Funkce absolutní hodnoty
- f(n)=∣n∣
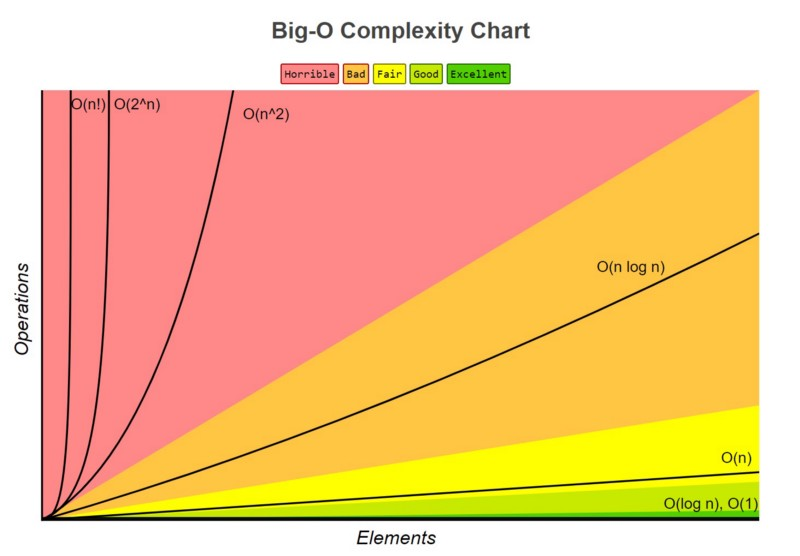
- Růst je lineární (O(n))
Funkce lineární
- f(n)=n
- y=ax+b
- Např. průchod spojovým seznamem
Kvadratická funkce
- f(n)=n2
- Např. neefektivní třídící algoritmy (bubble sort)
Kubická funkce
Mocniná funkce se záporným exponentem
- f(n)=n−1
- tzv. nepřímá úměrnost
- Rozdílné pokud je exponent sudý/lichý
Exponenciální funkce
- b>1 - rostoucí
- b<1 - klesající
- Růst zhruba O(2n) (v praxi téměr nepoužitelná)
- Např. SAT, obecně brute-force
Logaritmická funkce
- f(n)=log(n)
- Velmi dobře použitelný algoritmus v praxi
- Např. dělení problému na poloviny, binární hledání
Logaritmicko-lineární funkce
- f(n)=n⋅log(n)
- Např. lepší třídící algoritmy (quick sort, merge sort)
Funkce faktoriál
- f(n)=n!
- Z hlediska O-notace nejhorší možnost rychlosti růstu
- Např. Počet možných permutací množiny, TSP
Funkce konstantní
Funkce sin, cos, tag, cotag
- f(x)=sin(x)
- f(x)=cos(x)
- f(x)=tg(x)
- f(x)=cotg(x)


