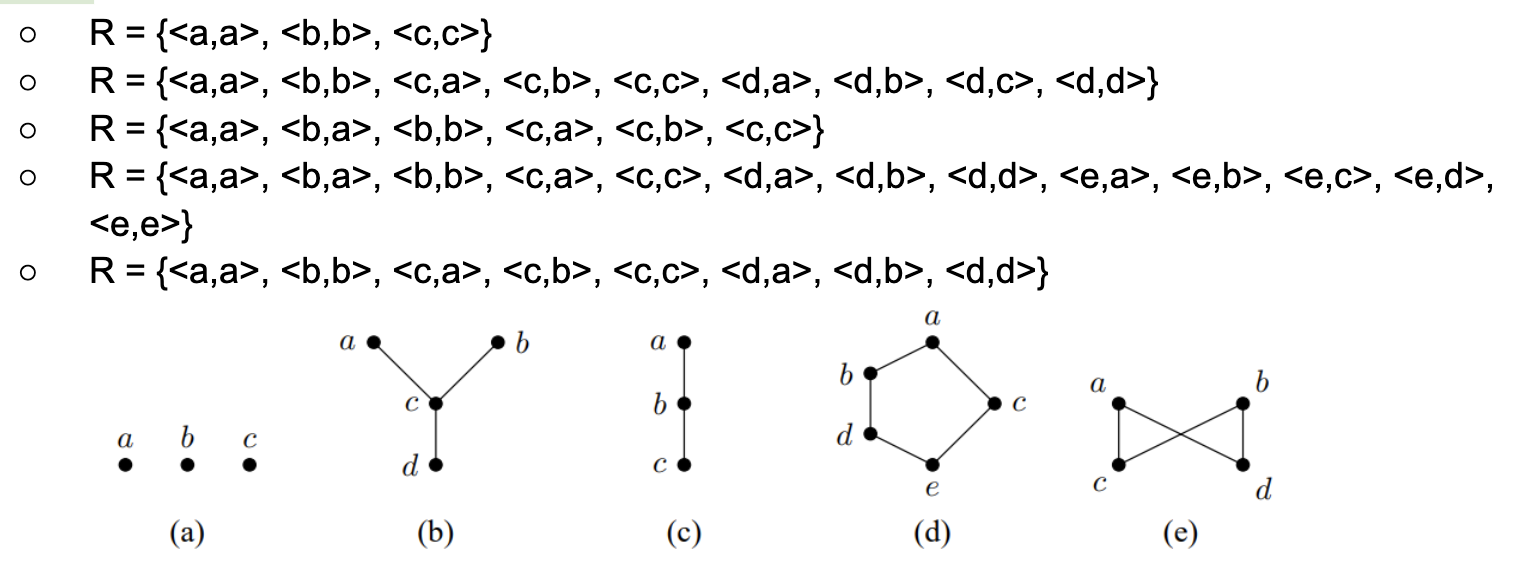disk1 svazy hasseovy-diagramy uspořádání
Uspořádání
- Uspořádání je matematický protějšek pojmu hierarchie
- Binární relace na množině se nazývá uspořádání, je-li reflexivní, antisymetrická a tranzitivní.
Tip
- Reflexivní - Každé z je totožné s , tedy
- Tranzitivní - Pokud a , pak i
- Antisymetrická - Pokud , pak neplatí , kromě pokud
-
kvaziuspořádání … reflexivní a tranzitivní binární relace na
-
uspořádání … antisymetrické kvaziuspořádání
-
ekvivalence … symetrické kvaziuspořádání
-
Úplné uspořádání se nazývá lineární uspořádání neboli řetězec
-
Pokud je relace uspořádání na množině , pak se nazývá se uspořádaná množina
-
Relaci uspořádání na obvykle značíme
- Místo píšeme
-
Uspořádání pořád ještě není formálním protějškem “uspořádání” na které jsme zvyklí při porovnání čísel, protože v uspořádané množině mohou stále existovat prvky, které jsou nesrovnatelné (značíme )
-
V lineárním uspořádání (řetězci) jsou každé dva prvky srovnatelné
- Můžeme lineární uspořádání chápat jako matematický protějšek pojmu “tradiční srovnání čísel”
-
Každá relace identity je uspořádání, které nazýváme antiřetězec (každé dva různé prvky z jsou nesrovnatelné ())
- Antiřetězce jsou nejmenší uspořádání, protože každé uspořádání na obsahuje
-
Relaci uspořádání “menší rovno” na číselných množinách nazýváme přirozené uspořádání čísel (je reflexivní, antisymetrické, tranzitivní a úplné), (nejedná se o jediné přirozené uspořádání čísel na číselných množinách)
-
Když je uspořádání na , pak (inverzní) je uspořádání na , které označujeme
Princip duality
V praxi to znamená, že pokud řeknu tvrzení pro nejmenší prvek v uspořádané množině , tak PLATÍ i pro největší prvek v uspořádaní množině
Znázornění uspořádání a pokrytí
-
Konečnou relaci uspořádání můžeme znázornit maticí, nebo orientovaným grafem, ale díky speciálním vlastnostem je můžeme znázorňovat mnohem přehledněji pomocí speciálních diagramů
-
Ke každému uspořádání na lze uvažovat odvozenou relaci definovanou předpisem
- , právě když a pro každé platí: pak
- Znamená že a zároveň neexistuje žádný prvek , který by se nacházel “mezi a .” (bezprostřední pokrytí prvků)
Info
Relaci nazýváme pokrytí příslušné
- čteme “x je pokryt y” nebo “y pokrývá x”
- , tedy relace je obsažena v uspořádání
- Relace pokrytí je: ireflexivní, asymetrická a NENÍ tranzitivní
Hasseův diagram
- Znázorňují konečné uspořádané množiny
- Složen z uzlů (prvky množiny ) a hran (vyznačující relaci pokrytí )
- Pravidla:
- Je-li , nakreslíme uzel níže než uzel
- Je-li , propojíme uzel a úsečkou
- Je vhodné, aby se hrany nekřížili
Příklad hasseova diagramu
Význačné prvky v uspořádaných množinách a jejich vztahy
-
Nechť je uspořádaná množina. Prvek se nazývá:
- minimální, jestliže pro každý platí: pokud , pak
- nejmenší, jestliže pro každý (je pouze jeden)
- maximální, jestliže pro každý platí: pokud , pak
- největší, jestliže pro každý (je pouze jeden)
-
Pokud je nejmenší, pak bude i minimální (obráceně neplatí)
-
Pokud je největší, pak bude i maximální (obráceně neplatí)
-
Nechť je uspořádaná množina. Pak platí:
- V existuje nejvýše jeden největší a jeden nejmenší prvek
- Je-li největší (nejmenší) prvek, pak je také maximální (minimální) a žádné další maximální (minimální) prvky se v nevyskytují
- Pokud je lineární uspořádání, pak je největší (nejmenší) prvek, právě když je maximální (minimální)
Horní a dolní mez
-
Nechť je uspořádaná množina a . Definujeme množiny
- platí pro každé
- Nazývá se dolní kužel množiny v
- Vznikne uspořádaná množina
- platí pro každé
- Nazývá se horní kužel množiny v
- Vznikne uspořádaná množina
- platí pro každé
-
V horním/dolním kuželu můžeme najít, pokud existuje, nejmenší (největší) prvek.
-
Nechť je uspořádaná množina a
- Pokud má největší prvek, pak se nazývá infimum a označuje se
- Pokud má nejmenší prvek, pak se nazývá supremum a označuje se
Svazy
- Na základě existence infima či suprema ke každým dvěma prvkům definujeme speciální uspořádané množiny zvané polosvazy a svazy
- Nechť je uspořádaná množina.
- Pokud pro každé existuje , pak nazveme průsekový polosvaz
- Pokud pro každé existuje , pak nazveme spojový polosvaz
- Je-li průsekový i spojový polosvaz, pak nazveme svaz
- Svaz … pro každé dva prvky existuje supremum i infimum
- Každý konečný svaz má největší a nejmenší prvek