Co a k čemu jsou grafy
- Grafy představují místa a spojení mezi nimi, mají řadu různorodých aplikací
- Teorie grafů se zabývá situacemi spojenými s grafy
- Hledání nejkratší cesty
- Problém obchodního cestujícího
- Problém barvení grafu (problém 4 barev)
- Eulerovy cesty a kružnice
- atd.
- Objekty se nazývají vrcholy, spojení pak hrany
- Graf je dán množinou vrcholů a množinou hran mezi nimi (dvojice )
- Nezáleží-li na orientaci hran, nazývá se graf neorientovaný, v opačném případě se nazývá orientovaný
Neorientovaný graf
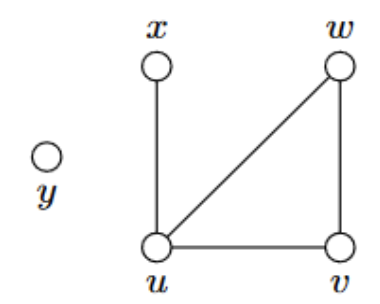
- Na obrázku je neorientovaný graf který má vrcholy a
- Vrcholy jsou znázorněny kroužky. Úsečky znázorňují hrany.
- Protože v neorientovaném grafu nemají hrany orientaci, můžeme hranu mezi vrcholy reprezentovat neuspořádanou dvojicí, tedy dvouprvkovou množinou napr.
- Komponenta neorientovaného grafu je každý jeho maximální souvislý podgraf.
- Komponenty tvoří rozklad grafu
Orientovaný graf
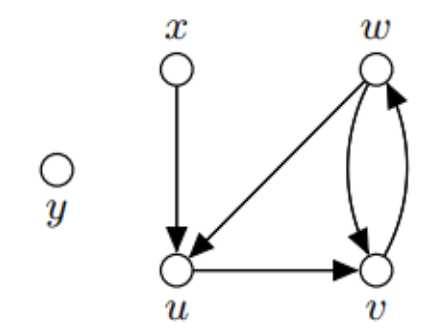
- Na obrázku je orientovaný graf který má opět vrcholy a
- Hrany jsou orientované a jsou znázorněny šipkami. Reprezentujeme je tedy uspořádanou dvojicí např.
-
Neorientovaný graf je dvojice , kde je neprázná množina vrcholů a je množina dvouprvkových množin vrcholů, tzv. neorientovaných hran
-
Orientovaný graf je dvojice , kde je neprázdná množina vrcholů a je množina uspořádaných dvojic vrcholů, tzv. orientovaných hran
-
u říkáme, že hrana spojuje a
-
u říkáme, že hrana vede z do
-
u obou případů se nazývají vrcholy koncové
-
Graf , a se nazývají množina vrcholů a množina hran grafu a značí se a
-
Graf můžeme zadat přímo obrázkem, což může být přehlednější než jeho popis jakožto struktury
-
K orientovanému grafu je třeba někdy uvažovat graf, který vznikne zanedbáním orientace stran. Říká se mu symetrizace orientovaného grafu
-
Symetrizace orientovaného grafu je neorientovaný graf , kde
- právě když nebo
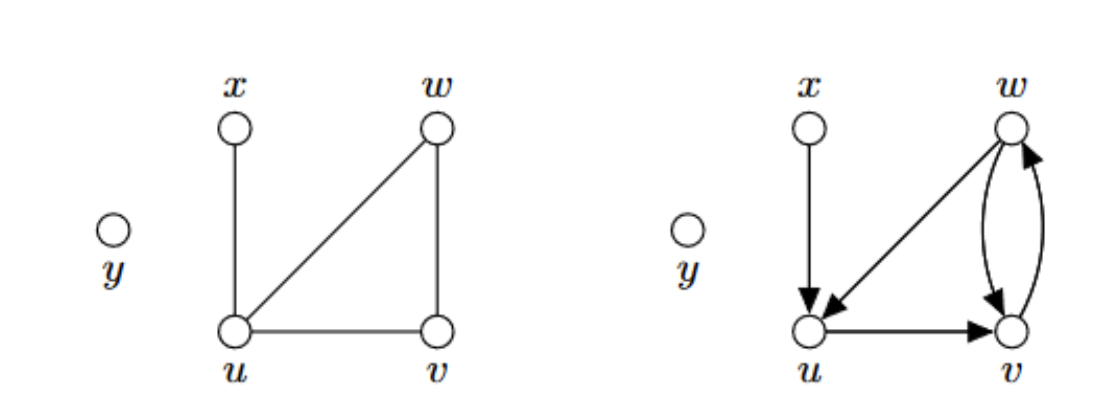
- Graf vlevo je symetrizací grafu vpravo
Izomorfismus
-
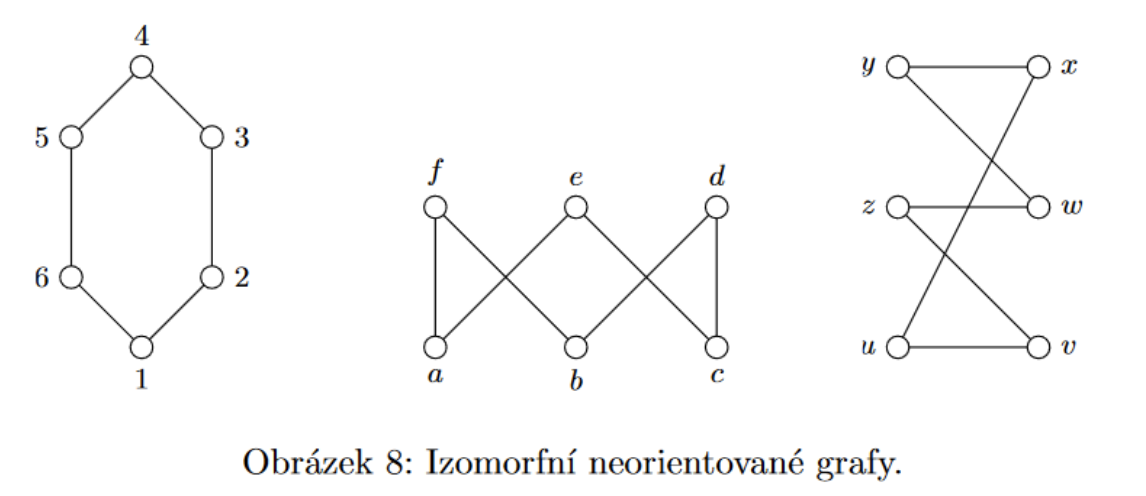
Obrázek daného grafu není určen jednoznačně. Dva různé obrázky přitom mohou popisovat v zásadě stejné grafy, byť to na první pohled není patrné.
-
V případě, že graf je dán obrázkem, mohou se obrázky dvou v zásadě stejných grafů lišit rozmístěním vrcholů, zakreslením hran, popř. také označením vrcholů.
-
Grafy, které mají stejnou strukturu, se nazývají izomorfní.
- Značíme
-
Nechť a jsou neorientované grafy. Bijekce se nazývá izomorfismus do , pokud pro každé vrcholy je
- právě když
-
Nechť a jsou orientované grafy. Bijekce se nazývá izomorfismus do , pokud pro každé vrcholy je
- právě když
- právě když
Stupeň vrcholu
- Počet hran, které z daného vrcholu vycházejí
- Stupeň vrcholu grafu je počet hran, pro které je koncovým vrcholem, značí se
- Počet vrcholů lichého stupně je v libovolném grafu sudý.
- V grafu je
Skóre grafu
- Jako skóre grafu se označuje libovolně uspořádaná posloupnost stupňů jeho vrcholů
- Dvě skóre jsou stejná pokud jedno dostaneme permutací druhého (nezáleží na pořadí)
- Věty pro vztahy 2 grafů a skóre
- Pokud jsou skóre jiná grafy nemohou být izomorfní
- Pokud jsou 2 grafy izomorfní musí mít stejná skóre
- Obrácené implikace NEplatí (viz obrázek, stejná skóre, jiné grafy)
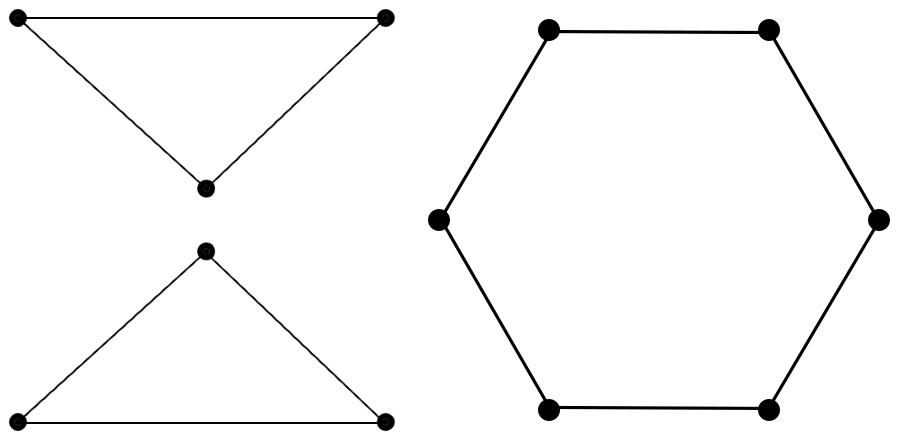
Souvislost v grafu
- Graf je souvislý pokud mezi každými 2 uzly a existuje sled z do
Podgrafy
- Části grafů se nazývají podgrafy
- (Orientovaný nebo neorientovaný) graf je podgrafem grafu , právě když a . Podgraf grafu se nazývá indukovaný, právě když obsahuje každou hranu z , jejíž oba koncové vrcholy patří do
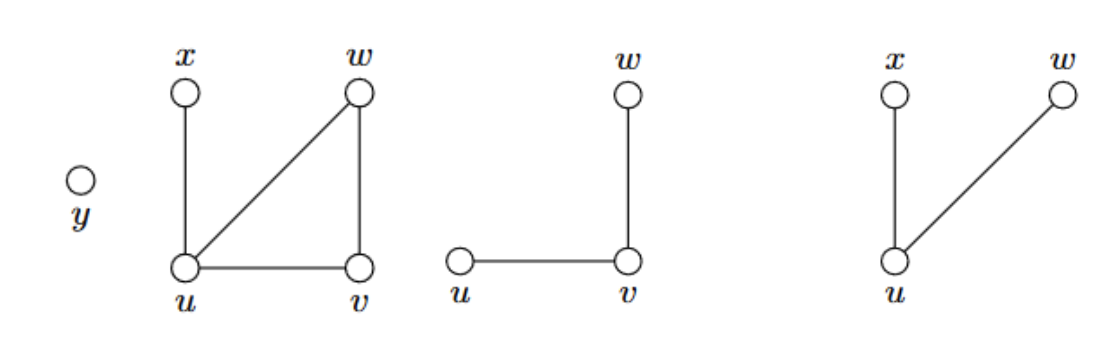
- Graf uprostřed společně s grafem vpravo jsou podgrafy grafu vlevo, přitom graf uprostřed není indukovaný protože mu chybí hrana , graf vpravo je.
Cestování v grafech
-
Sled v grafu je posloupnost kde jsou vrcholy, jsou hrany a platí, že
- pro , je-li graf neorientovaný
- pro , je-li graf orientovaný
-
Číslo se nazývá délka sledu
-
Sled se nazývá:
- uzavřený, je-li
- tah, neopakuje-li se v něm žádná hrana
- cesta, neopakuje-li se v něm žádný vrchol
- kružnice, je-li tahem, a s výjimkou vrcholů a jsou každé dva vrcholy různé
-
vzdálenost z vrcholu do vrcholu je délka cesty z do , které má ze všech cest z do délku nejmenší