Merge sort a jeho složitost

• Třídění sléváním (slučováním)
• Algoritmus “rozděl a panuj”
  • Setřiď levou polovinu pole, setřiď pravou polovinu pole, slij obě poloviny
• Složitost algoritmu v nejhorším případě: $\Theta (n\log n)$
• Out-of-place třídění
• Stabilní algoritmus porovnávání

Merge-Sort(A, p, r)
	if p<r
		then q <- floor((p+r)/2)
			 Merge-Sort(A, p, q)
			 Merge-Sort(A, q+1, r)
			 Merge(A, p, q, r)

Merge(A, p, q, r)
	n1 <- q-p+1
	n2 <- r-q
	vytvoř nová pole L[0 ... n1] a R[0 ... n2]
	for i <- 0 to n1-1
		do L[i] <- A[p+i]
	for j <- 0 to n2-1
		do R[j] A[q+1+j]
	L[n1] <- infinity
	L[n2] <- infinity
	i <- 0
	j <- 0
	for k <- p to r
		do if L[i] <= R[j]
			then A[k] < L[i]
				 i <- i+1
			else A[k] <- R[j]
				 j <- j+1

Příklad

Odůvodnění složitosti MergeSort

• Při počítání časové složitosti algoritmu Merge Sort dojedeme k pojmu tzv. rekurence
• Rekurence se objevuje u algoritmů, kde dochází k rekurzivním voláním. Rekurence je rovnice (nebo nerovnost), která popisuje funkci z hlediska její hodnoty na menších částech. Příkladem může být tento tvar $T(n)=2\cdot T(\frac{n}{2})+n$.
• Pro zjednodušení určitého typu rekurence slouží Master Theorem (viz dále) $\text{Prˇedpis, kteryˊ rˇesˇıˊ MT:}T(n)=a\cdot T(\frac{n}{b})+f(n)$

Tip

• Master Theorem řeší následující typ rekurence.
• $T(n)=a\cdot T(\frac{n}{b})+f(n)$

1. Pokud $f(n)=O(n^{lo{g}_{b}a-ϵ})$ pro nějaké $ϵ>0$, pak $T(n)=\text{Uptheta}(n^{lo{g}_{b}a})$
2. Pokud $f(n)=\text{uptheta}(n^{lo{g}_{b}a})$, pak $T(n)=\text{Uptheta}(n^{lo{g}_{b}a}\cdot log(n))$
3. Pokud $f(n)=\Omega (n^{lo{g}_{b}a+ϵ})$ pro nějaké $ϵ>0$ a pokud $af(\frac{n}{b})\le cf(n)$ pro nějaké $c<1$ a dostatečně velké $n$, pak $T(n)=\text{Uptheta}(f(n))$.

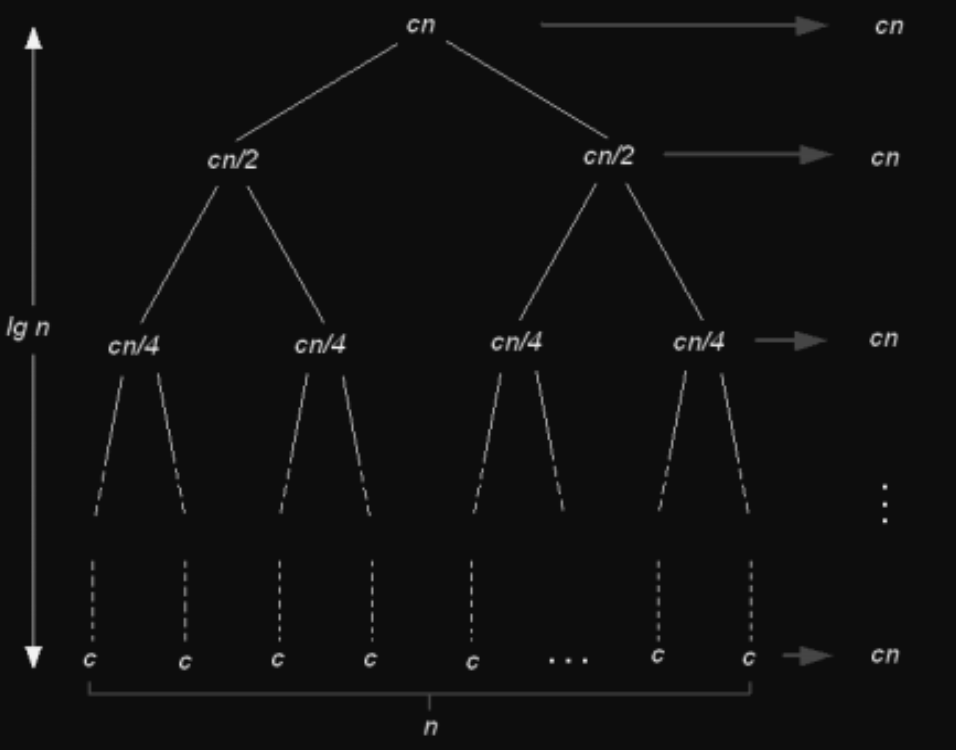
• Složitosti merge sortu potom můžeme vyjádřit následovně (pomocí rovnic i stromu)
  • $T(n)=c$ pro $n=1$
  • $T(n)=2T(\frac{n}{2})+cn$ pro $n>1$
  • $T(n)=cn\log n+cn=\Theta (n\log n)$ (podle Master theoremu)
  • 

Navigace

Předchozí: Quick sort a jeho složitost Následující: Heap sort a jeho složitost Celý okruh: 1. Teoretické základy informačních technologií