Konečné a nekonečné množiny, spočetné množiny, příklady, existence, nespočetné množiny, diagonální metoda

Konečná a nekonečná množina

• Množina $A$ je konečná pokud existuje $n\in \mathbb{N}$ a bijekce $f:\{1,2,...,n\}\to A$
  • Prvky můžeme seřadit do konečné posloupnosti
• Množina A je nekonečná pokud není konečná
• mohutnost (velikost) množiny … počet jejich prvků … $|A|$

Spočetná a nespočetná množina

• Množina $A$ je spočetná pokud je konečná nebo existuje bijekce $f:\mathbb{N}\to A$ (tzv. spočetně nekonečná)

• Základní množinou je identita $f(n)=n$ (bijekce $\mathbb{N}\to \mathbb{N}$)

• Množina ${\Sigma }^{\ast }$ všech řetězců nad abecedou $\Sigma =\{a_1,...,a_n\}$ je spočetná

• Nespočetná je množina pokud není spočetná

  • Musí být tedy určitě nekonečná, ale zároveň je ještě “větší” než $\mathbb{N}$
  • $\mathbb{R}$ i $2^{\mathbb{N}}$ jsou nespočetné

• Důkazy se obvykle provádí tzv. diagonální metodou

Tip

• Pro libovolnou nekonečnou množinu $A$ existuje injektivní zobrazení $f:\mathbb{N}\to A$.
• Neboli $A$ obsahuje nekonečnou spočetnou podmnožinu $f(\mathbb{N})$.

Diagonální metoda

• Důkaz se provádí sporem
• Předpokládáme že $2^{\mathbb{N}}$ je spočetná
• Pak existuje bijekce $f:\mathbb{N}\to 2^{\mathbb{N}}$, $f(i)=A_i$, a tedy posloupnost $A_1,A_2,...$ všech podmnožin množiny $\mathbb{N}$.
• Sestrojíme nyní množinu $B\subseteq \mathbb{N}$, která je různá od každé z $A_1,A_2,...$, to bude spor.
• Množinu $A_i$ reprezentujeme řádkem v kterém jsou $0$ a $1$

	1	2	3	4	…	j	…
$A_i$	0	0	1	0	…	$a_{ij}$	…

• Tedy $1,2,4\notin A_i$ a $3\in A_i$
• Uvažujme jako schéma hlavní diagonálu následující tabulky
• 
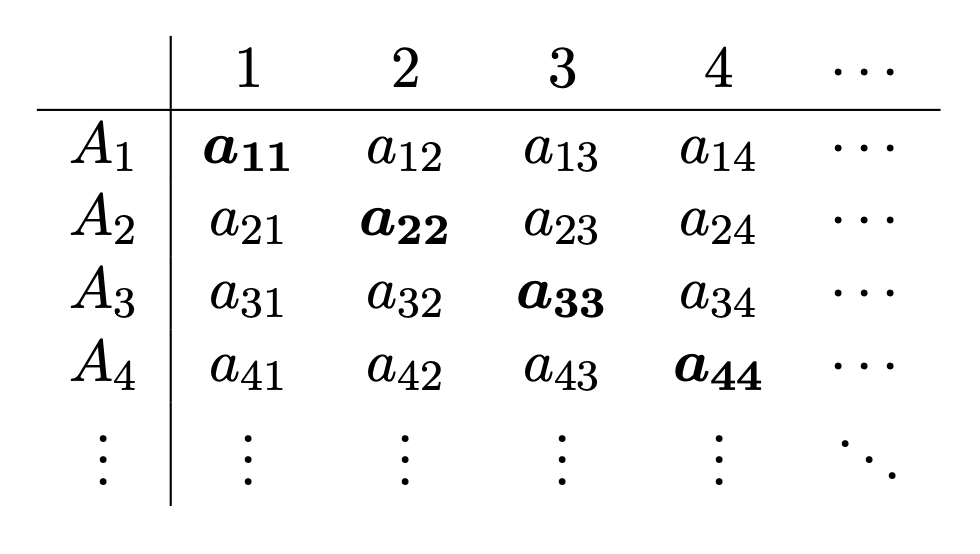
• Množinu $B$ definujeme jako množinu, které vznikne negací hlavní diagonály
• Tedy pro každé $i\in \mathbb{N}$ definujeme $b_i=1-a_i$, neboli $i\in B$ právě když $i\notin A_i$
• Pak $B$ je podmnožinou $\mathbb{N}$, ale $B\ne A_1,A_2,...$, protože $B$ a $A_i$ se liší v prvku $i$. $\square$