Dělitelnost, prvočísla, věty o jednoznačnosti

Dělitelnost

Definice

• Číslo $a$ je dělitelné číslem $b$ ($b\ne 0$), pokud existuje celé číslo $k$ takové, že: $a=k\cdot b$
• Zapisujeme: $b\mid a$ (čteme „$b$ dělí $a$“).

• Jedná se o binární relaci, pro které platí následující vlastnosti
  • $a,b,c\in \mathbb{Z}$
  1. $a\mid a$, $1\mid b$, $c\mid O$
  2. jestliže $a\mid b$ a $b\mid c$, pak i $a\mid c$
  3. jestliže $a\mid b$ a $b\mid c$, pak pro každé $x,y\in \mathbb{Z}$ platí $a\mid (bx+cy)$
• Relace dělitelnosti je uspořádání na množině $\mathbb{N}$
  • Relace má následující vlastnosti: reflexivitu (1), tranzitivitu (2) a antisymetrii ($a\mid b$ a $b\mid a$ pak $a=b$)

Největší společný dělitel (NSD)

• Největší číslo, které dělí čísla $a$ i $b$
• Efektivní metodou pro nalezené je Eukleidův algoritmus (odkaz zde)
• Pokud je $NSD=1$, pak jsou čísla nesoudělná

Nejmenší společný násobek (NSN)

• Nejmenší číslo, které je společným násobkem obou čísel
• Společný násobek je číslo, pro které platí: $x,y,n\in \mathbb{N}$ a $x\mid n$ i $y\mid n$
  • Z této množiny čísel vybereme nejmenší a to je NSN

Věta - souvislost NSD a NSN

Nechť $x,y\in \mathbb{N}$ pak platí $NSD(x,y)\cdot NSN(x,y)=x\cdot y$.

Prvočísla

Definice

Přirozené číslo $p$ se nazývá prvočíslo, jestliže $p\ne 1$ a $p$ je dělitelné jen a pouze čísly $1$ a $p$. Složené číslo je každé přirozené číslo $\ge 2$, které není prvočíslem.

Prvočísel existuje nekonečně mnoho.

Základní věta aritmetiky (jednoznačnost prvočíselného rozkladu)

Každé přirozené číslo $>1$ lze vyjádřit jednoznačně až na pořadí činitelů jako součin prvočísel.

*Poznámka: Prvočísla můžeme považovaz za základní kameny, z nichž můžeme pomocí operace násobení poskládat ostatní čísla.

• Důkaz ZVA by se provedl matematickou indukcí. Pro prvočísla je triviální, což by byl základní krok indukce, na který se pak dále naváže.

• Pro hledání malých prvočísel se dá využít algoritmus známý jako Eratosthenovo síto

  • 
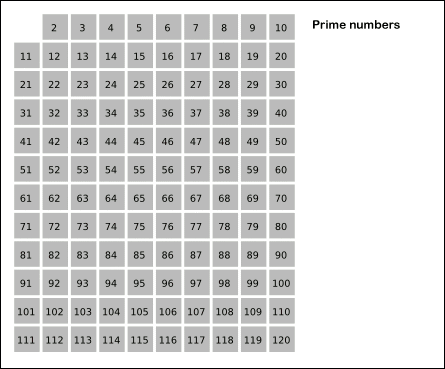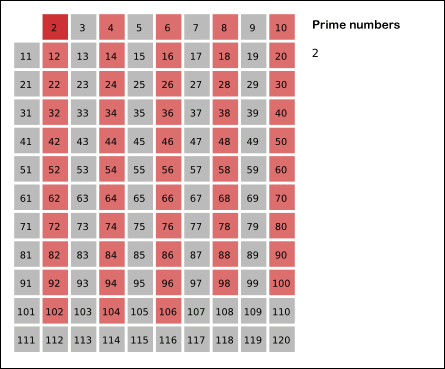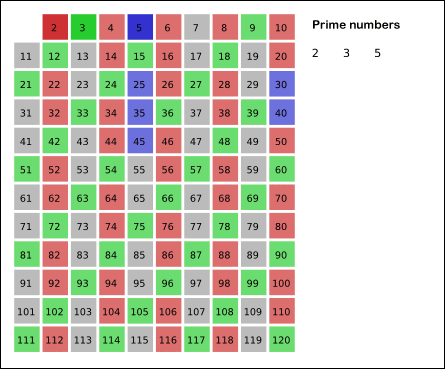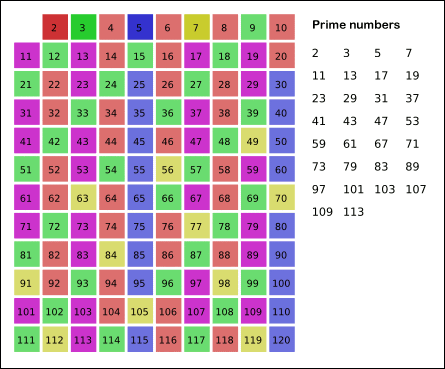
  • Postup algoritmu viz gif výše. Vstupem je seznam čísel, z kterého se od nejmenšího odebírají postupně čísla a jejich násobky. Pokud by odebírané číslo mělo být větší než odmocnina největšího čísla, tak algoritmus skončí). Neodebraná čísla jsou prvočísla.

Věty o jednoznačnosti

Věta o jednoznačnosti dělění se zbytkem

Pro $a,b\in \mathbb{Z},b\ne 0$ existují jednoznačně určená $q,r\in \mathbb{Z}$ tak, že $a=bq+r$ a $0\le r<b$.

• Číslu $r$ říkáme zbytek po celočíselném dělení, číslo $q$ je částečný podíl
  • $a\mathrm{mod}b=r$

Věta o jednoznačnosti zápisu přirozeného čísla v soustavě o základu $b$

Nechť $b>1$ je přirozené číslo. Pro každé $x\in \mathbb{N}$ existují jednoznačně určená čísla $a_n,a_{n-1},...,a_1,a_0$ přičemž $0\le a_i<b$, $a_n\ne 0$ tak, že $x=a_n{b}^n+a_{n-1}{b}^{n-1}+...+a_{1}b+a_0$.

• Pokud je základ soustavy větší než kolik máme číslic používáme písmena

Malá Fermatova věta

Pro každé prvočíslo $p$ a každé $a\in \mathbb{N}$ platí $a^p\equiv a(modp)$ Pokud navíc NSD($a$, $p$) = 1 pak $a^{p-1}\equiv 1$ (mod $p$)

Eulerova věta

Pokud $a$ a $n$ jsou nesoudělná čísla (tedy NSD$(a,n)=1$), pak: $a^{\phi (n)}\equiv 1$ (mod n)

Eulerova funkce

$\phi (n)$ … počet přirozených čísel menších než $n$ a s $n$ nesoudělných